1. 问题描述

  • 定义

    背包问题(来自于百度百科)

    有N件物品和一个容量为V的背包。第i件物品的重量是w[i]，价值是v[i]。求解将哪些物品装入背包可使这些物品的重量总和不超过背包容量，且价值总和最大。

  • 分析

    1. 我们要获取这个问题的最优解, 也就是最佳的价值
    2. 可以使用贪婪算法对其进行一个遍历
    3. 在遍历时, 每当遇到一个物品的时候, 可分为装这个东西, 还是不装这个东西.
    4. 遍历时, 我们可以将这个问题产生的结果构成一颗二叉树, 因为每当遇到一个物品的时候,我们总是能将其分解成, 装这个物品, 还是不装这个物品.
    5. 当我们遍历完成后, 所产生的最优解一定是最后的叶子结点中的一个.

2. 计算方法

  • DP计算公式
    DP公式

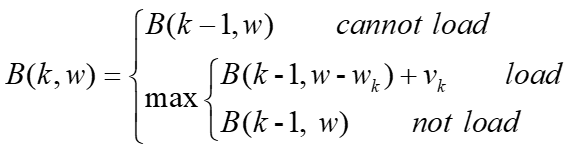
    • 对上述公式的说明
      • B(k, w) 表示的是我们的背包问题的最优解, 其中k, 表示第k个物品, w表示背包里面还能装的下的重量.
      • B(k - 1, w - wk) + vk 的意思就是, 如果装的话, 将这个第k个物品的重量(wk) 装上, 加上这个物品的一个价值, 此时背包中还能装下的质量为w - wk
      • 如果不装的话, 此时背包里面就剩余w个重量

  • 最优解的表格, 我们以下面这个例子来说明

    重量 2 3 4 5 9
    价值 3 4 5 8 10
    编号 1 2 3 4 5
    背包容量 20

  • 对于以上这个例子, 我们可以得到下面这个表格
    最优解集

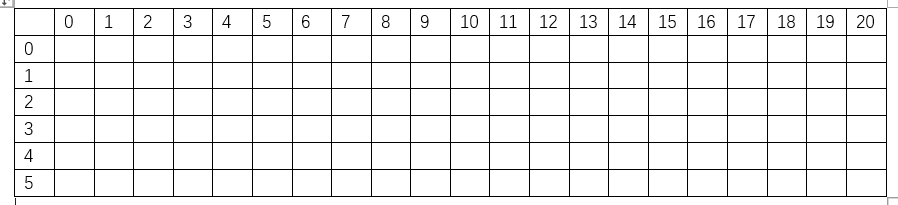
    • 对于以上这个表格
      • 其中行表示的是物品的编号, 列表示的是背包所占有的容量
      • 每一个格子中的数字表示最大的数字, 就是我们的最优解
      • 比如行为3, 列为5的时候, 格子中表示的数字就是, 只占用5个背包容量, 只装前三个物品, 能够得到的最大的价值
      • 那么对于整一个问题的最优解就是我们在所有的物品里面做出选择, 利用所有的背包容量来装, 得到的最大的价值, 就是表格的最右下角的那个格子的值

  • 下面我们就用代码来求解一下上述的例子

3. 代码

下面使用c语言实现一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <stdio.h>
#include <stdlib.h>
#define N 6  // rows is 6
#define W 21 // column is 21

// global varables
int Bs[N][W] = {0}; // initialize the table which can show our max value
int weight[6] = {0, 2, 3, 4, 5, 9}; // weight of every goods
int values[6] = {0, 3, 4, 5, 8, 10}; // value of every goods

// calculate max value and fill the table
void knapsack() {
	int k, C;// c is capacity, k is number of goods
	for (k = 1; k < N; k++) {
		for (C = 1; C < W; C++) {
			// cannot load
			if (weight[k] > C) {
				Bs[k][C] = Bs[k - 1][C];
			}
			else {
				// decide which is better if we load current goods
				int value1 = Bs[k - 1][C - weight[k]] + values[k];
				int value2 = Bs[k - 1][C];
				if (value1 > value2) {
					Bs[k][C] = value1;
				}
				else {
					// not load
					Bs[k][C] = value2;
				}
			}
		}
	}
}


// show the max value table
void printBs() {
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < W; j++) {
			printf("%2d ", Bs[i][j]);
		}
		printf("\n");
	}
}

int main(int argc, char const *argv[])
{
	knapsack();
	// show the max values
	printf("The max value is %d\n", Bs[5][20]);
	printf("The max values table is the following \n");
	printBs();
	return 0;
}

4. 总结

  • 以上代码虽然能够求得一个最优解, 最大值, 但是我们并不能直观的展示具体装了那个物品.
  • 这个方法, 使用了一个一个遍历, 对于每一个物品以及每一个容量都进行了遍历迭代, 复杂度较高
  • 会再继续学习, 取得更好的解法